文章为徐亦达机器学习课程中的隐马尔可夫模型视频笔记，课程链接点击这里，课件下载地址点击这里。

Part 1 基本概念介绍

HMM模型适用于序列问题，首先我们通过一个股票的案例来引入这个算法，在时间序列下股票行情和涨跌观测值的状态图：

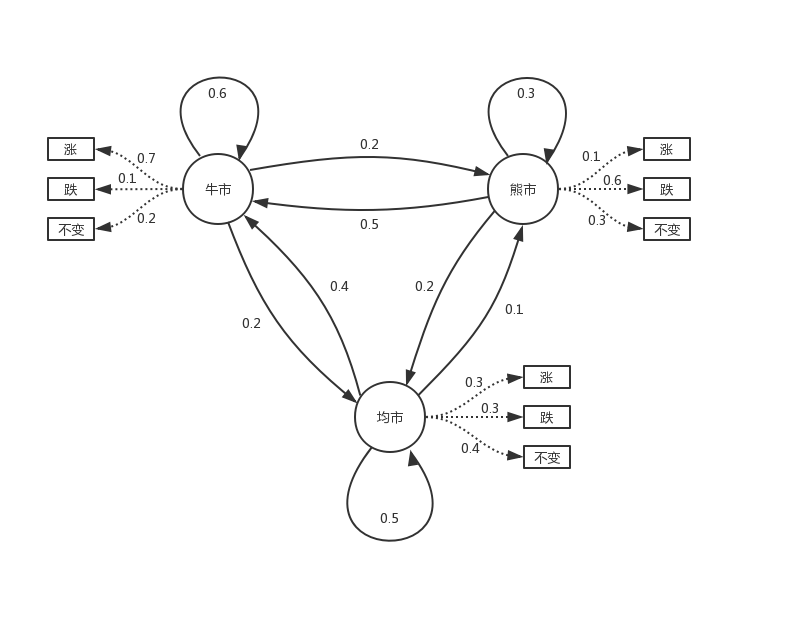
由图中可以看出，股市的行情分成牛市、熊市和均市，这三种行情是可以互相转化的，并且互相转化是有一定的概率的。

由于股市的现在的行情高低并不能判断股市的未来涨跌，因此是一种隐藏状态，计作隐状态 $q$ ，并且在每一个时间点的状态我们可以表示成 $q_t$ ，同时 隐状态之间转化的概率称为转移概率 。

而我们可以观测到的是现在股市的涨跌，所以我们将涨跌或者是不变看成是观测值 $y$ ，某一时刻的观测值可以表示成$y_t$， 同时在隐状态中得到观测值的概率称为发射概率 。

假设隐状态 $q_t$ 的转移概率只与隐状态 $q_{t-1}$ 有关，公式表示为： $$ p\left(q_{t} \mid q_{1}, \ldots, q_{t-1}, y_{1}, \ldots, y_{t-1}\right)=p\left(q_{t} \mid q_{t-1}\right) $$ 假设观测值 $y_t$ 的概率只与隐状态 $q_t$ 有关，公式表示为： $$ p\left(y_{t} \mid q_{1}, \ldots, q_{t-1}, q_{t}, y_{1}, \ldots, y_{t-1}\right)=p\left(y_{t} \mid q_{t}\right) $$ 隐状态和观测值的关系我们可以由下概率图表示：

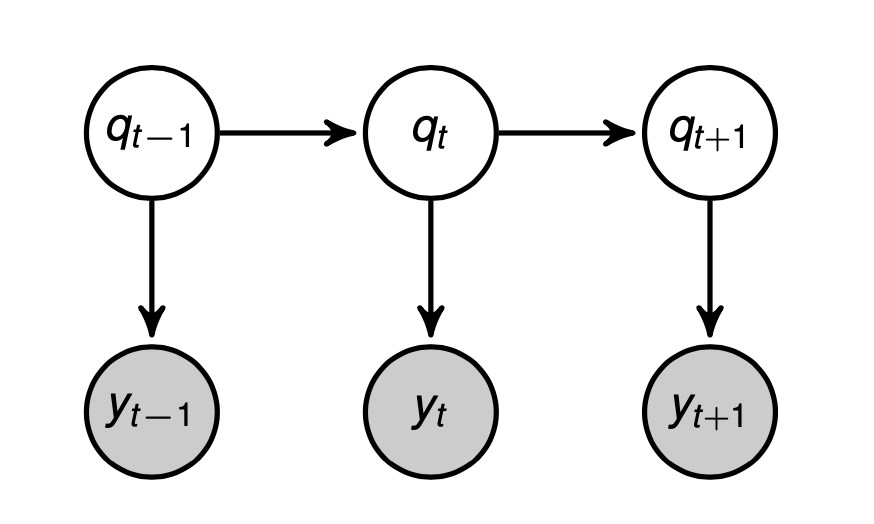
根据下概率图模型可知，观测值 $y$ 之间具有独立性，即： $$ p\left(y_{t} \mid y_{t-1}\right) = p\left(y_{t}\right) $$ 隐状态之间的转移概率可用矩阵表示，即： $$ A=\left[\begin{array}{lll} 0.6 & 0.2 & 0.2 \\ 0.5 & 0.3 & 0.2 \\ 0.4 & 0.1 & 0.5 \end{array}\right] $$ 例如，第一行表示牛市状态下转移到另外一个状态的概率，0.6表示下一个状态是牛市的概率，剩下的0.2和0.2分别表示牛市转到熊市和均市的概率，矩阵的第一列表示转移到牛市状态的概率，第二列表示转移到熊市的概率，第三列表示转移到均市的概率。每一行表示某个状态，所以说每一行元素相加的值为1。

使用概率公式表示为： $$ A_{k\times k}=\left[\begin{array}{ccc} P\left(q_{t}=1 \mid q_{t-1}=1\right) & \cdots & P\left(q_{t}=k \mid q_{t-1}=1\right) \\ \vdots & \ddots & \vdots \\ P\left(q_{t}=1 \mid q_{t-1}=k\right) & \cdots & P\left(q_{t}=k \mid q_{t-1}=k\right) \end{array}\right] $$ 每个隐状态得到观测值的概率被称为发射概率矩阵$B$，即： $$ B=\left[\begin{array}{lll} 0.7 & 0.1 & 0.2 \\ 0.1 & 0.6 & 0.3 \\ 0.3 & 0.3 & 0.4 \end{array}\right] $$ 使用概率公式表示为： $$ B_{k} * m=\left[\begin{array}{ccc} P\left(y_{t}=1 \mid q_{t}=1\right) & \cdots & P\left(y_{t}=m \mid q_{t}=1\right) \\ \vdots & \ddots & \vdots \\ P\left(y_{t}=1 \mid q_{t}=k\right) & \cdots & P\left(y_{t}=m \mid q_{t}=k\right) \end{array}\right] $$

重点：同时对于HMM模型，隐状态$q$需要是离散的，对于观测值$y$可以是离散的也可以是连续的。

Part 2 模型参数

上述HMM模型的概率矩阵在现实中需要从观测数据中求解，因此可以使用极大似然估计的方法得到模型参数。

首先 ，我们假设上述概率矩阵的参数已知，即已知隐状态之间的转移概率$A$和每个隐状态得到观测值的发射概率矩阵$B$。

其次 ，已知观测序列$y_1,y_2,y_3$。

重点：HMM适用于序列问题，即观测值具有连续性。

观测序列$y_1,y_2,y_3$的概率使用公式表示为： $$ P\left(y_{1}, y_{2}, y_{3}\right)=\sum_{q_{1}=1}^{K} \sum_{q_{2}=1}^{K} \sum_{q_{3}=1}^{K} P\left(y_{1}, y_{2}, y_{3}, q_{1}, q_{2}, q_{3}\right) $$ 对于观测序列$y_1,y_2,y_3$对于的隐状态$q_1,q_2,q_3$所有可能性下得到观测序列$y_1,y_2,y_3$的概率求和。

又，根据贝叶斯公式和马尔可夫性质： $$ \begin{align*} P\left(y_{1}, y_{2}, y_{3}, q_{1}, q_{2}, q_{3}\right)&=P\left(y_{3} \mid y_{1}, y_{2}, q_{1}, q_{2}, q_{3}\right) \times P\left(y_{1}, y_{2}, q_{1}, q_{2}, q_{3}\right) \\ &=P\left(y_{3} \mid q_{3}\right) \times P\left(y_{1}, y_{2}, q_{1}, q_{2}, q_{3}\right) \\ &= P\left(y_{3} \mid q_{3}\right) \times P\left(q_{3} \mid q_{2}\right) \times P\left(y_{2} \mid q_{2}\right) \times P\left(q_{2} \mid q_{1}\right) \times P\left(y_{1} \mid q_{1}\right) \times P\left(q_{1}\right) \end{align*} $$ 其中：

$P\left(y_{3} \mid q_{3}\right), P\left(y_{2} \mid q_{2}\right),P\left(y_{1} \mid q_{1}\right)$为发射概率矩阵$B$的中的参数；

$P\left(q_{3} \mid q_{2}\right),P\left(q_{2} \mid q_{1}\right)$为隐状态之间的转移概率$A$矩阵的参数；

$P\left(q_{1}\right)$为初始概率，定义为$\pi$。

则，一个HMM模型的所有参数$\lambda$表示为： $$ \lambda={A, B, \pi} $$

Part3 模型参数估计

对于模型参数估计，我们最常用的方法是极大似然估计。其原理是：假设当前观测序列出现的概率最大，从而根据观测序列将模型参数当作未知数，对观测序列出现的概率求最大值，满足最大值时的参数即为所求$\lambda$。

公式表示为： $$ \lambda_{M L E}=\arg \max P(Y \mid \lambda) $$ 根据Part2的推导可知（$a$为转移概率矩阵元素和$b$为发射概率矩阵）： $$ \begin{align*} P(Y \mid \lambda)&=\sum_{q_{1}=1}^{k} \ldots \sum_{q_{T}=1}^{k} P\left(q_{1}\right) P\left(y_{1} \mid q_{1}\right) P\left(q_{2} \mid q_{1}\right) \ldots P\left(q_{t} \mid q_{t-1}\right) P\left(y_{t} \mid q_{t}\right) \\ &=\sum_{q_{1}=1}^{k} \cdots \sum_{q_{T}=1}^{k} \pi\left(q_{1}\right) \prod_{t=2}^{T} a_{q_{t-1}, q_{t}} \cdot b_{q_{t}}\left(y_{t}\right) \end{align*} $$ 对于上式求最大值，则计算复杂度为$k^T$。

Part4 优化参数估计计算复杂度

对于上式的计算，我们可以用类似动态规划的方法对以往的计算状态进行保存，通过迭代的方法求出$P(Y \mid \lambda)$。

参考资料

[1]徐亦达机器学习：Hidden Markov Model 隐马尔可夫模型(HMM). https://www.bilibili.com/video/BV1BW411P7gV

[2]徐亦达机器学习课程课件. https://github.com/roboticcam/machine-learning-notes/blob/master/files/dynamic_model.pdf

[3]隐马尔科夫模型(HMM)算法的理解与超详细推导. https://blog.csdn.net/Oscar6280868/article/details/88550586