Gaussian Process Regression
高斯过程是机器学习领域中的一个重要模型,学习高斯过程需要预先学习概率与统计、贝叶斯回归、多元统计分析(协方差、相关系数)的内容。
1 什么是高斯过程
1.1 参数模型与非参数模型
在统计学中,参数模型通常假设总体服从某个分布,这个分布可以由一些参数确定,如正态分布由均值和标准差确定,在此基础上构建的模型称为参数模型;非参数模型对于总体的分布不做任何假设或者说是数据分布假设自由,只知道其分布是存在的,所以就无法得到其分布的相关参数,只能通过非参数统计的方法进行推断。
对于参数模型。 通过固定大小的参数集(与训练样本数独立)概况数据的学习模型称为参数模型。不管你给与一个参数模型多少数据,对于其需要的参数数量都没有影响。
常见的参数机器学习模型有:
- 逻辑回归(logistic regression)
- 线性成分分析(linear regression)
- 感知机(perceptron)
对于非参数模型。 由于非参数机器学习算法对目标函数形式不做过多的假设,因此算法可以通过对训练数据进行拟合而学习出某种形式的函数。当你拥有许多数据而先验知识很少时,非参数学习通常很有用,此时你不需要关注于参数的选取。
常见的非参数机器学习模型有:
- 决策树
- 朴素贝叶斯
- 支持向量机
- 神经网络
重点:高斯过程是不一样的非参数模型的类型。 不同于参数模型,高斯过程可以直接估计一个结果分布。高斯过程基于贝叶斯流程,在先验分布的基础上获得多个观测值后,更新后验分布。
1.2 可视化与数学定义
高斯过程可表示为连续的高斯分布,每一维按时间线展开,就得到一个高斯分布的曲线。这个曲线中的每一个点都对应了一个一维的高斯分布,而每个高斯分布都有一个均值和方差,故高斯过程中每个点对应一个均值和方差。如下图所示。图片来源于高斯过程可视化项目(http://www.infinitecuriosity.org/vizgp/)。
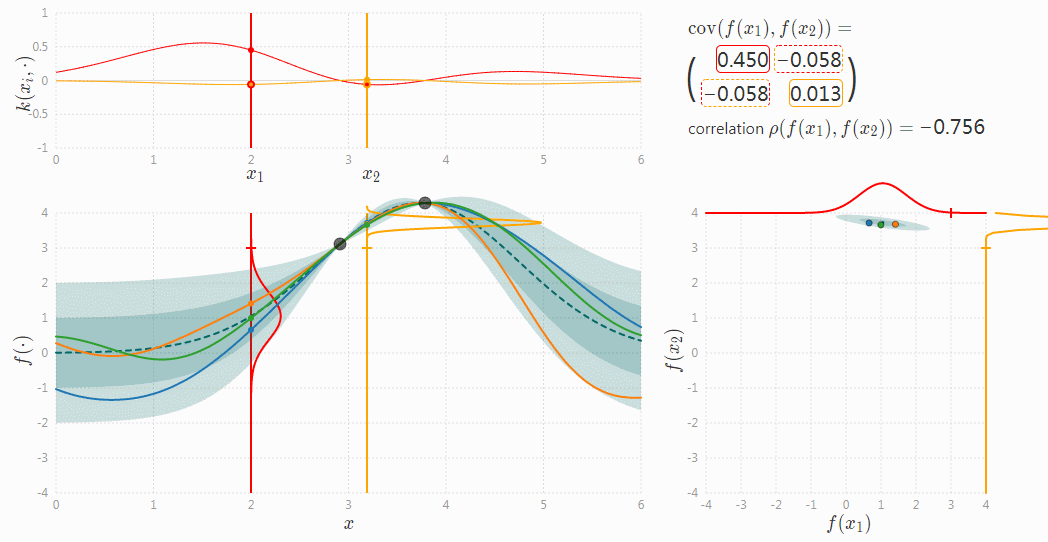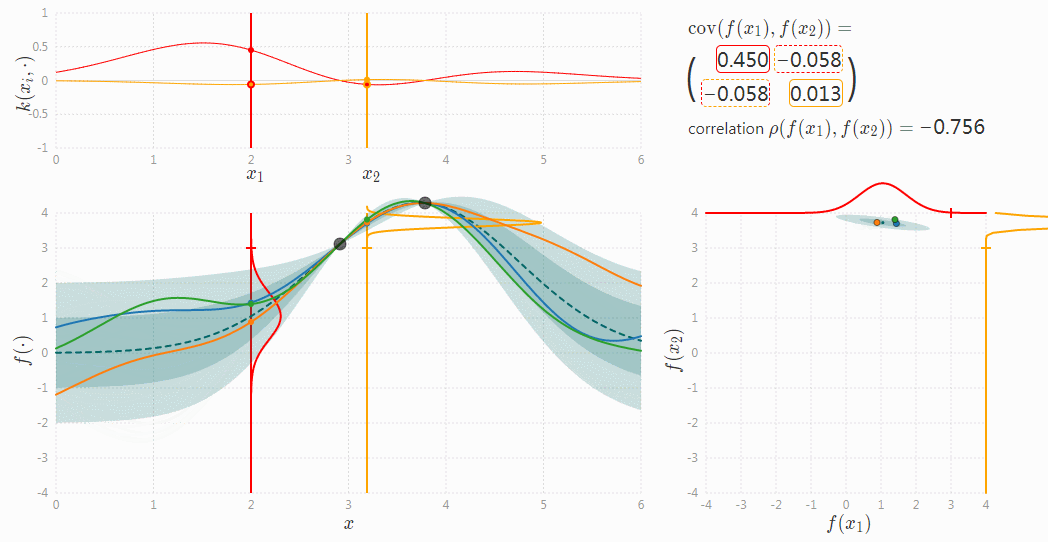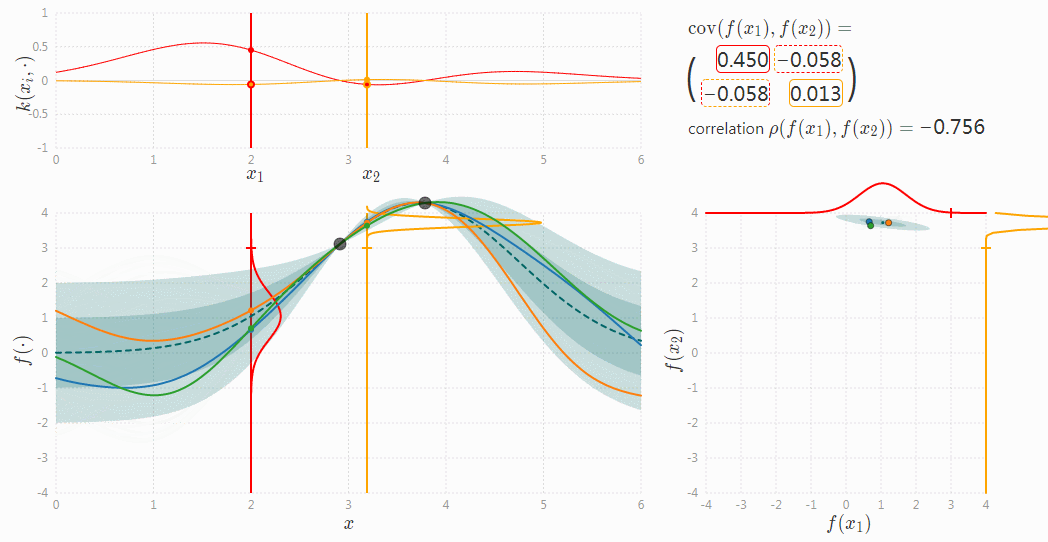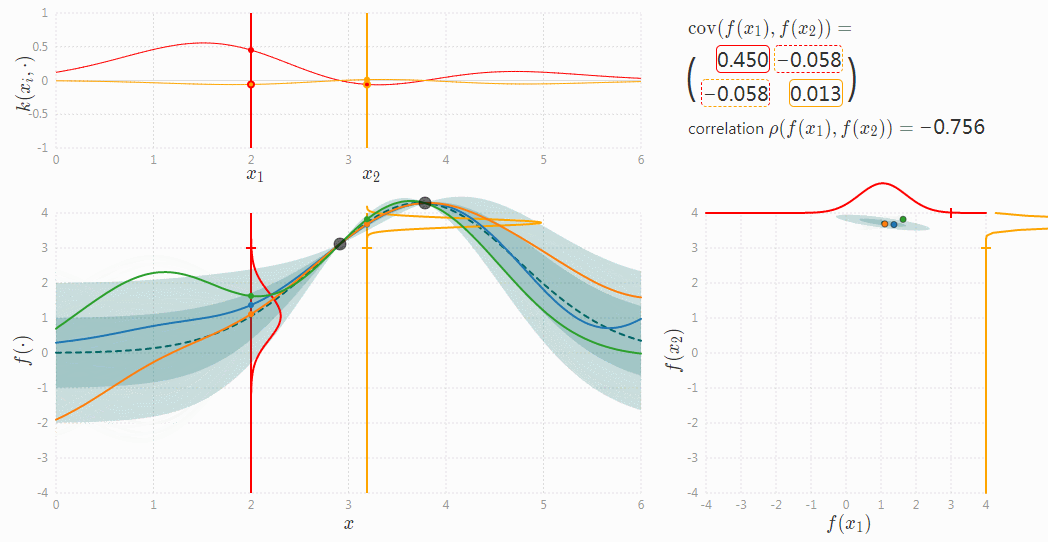
总的来说,一个高斯过程可以由一个均值函数和一个协方差函数来确定,即: \[ h(x) \sim N\left(\mu(x), \sigma\left(x\right)\right) \\ f(x) = h(x) + \epsilon, \epsilon \sim \mathcal{N}(0, \sigma_\epsilon) \] 均值函数为 \(\mu(x)\) ,表示为高斯分布的均值。
2 高斯过程回归
2.1 什么是高斯过程回归
高斯过程回归是用高斯过程解决回归问题的一种方法,只需要相对少量的样本数据就可以获得相对不错的模型效果。
举个例子,在给定数据集X、Y的情况下: \[ \begin{align*} X&=[3\quad 1\quad 4\quad 5\quad 9] \\\ Y&=[-0.99\quad 0.54\quad -0.65\quad 0.28\quad -0.91] \end{align*} \] 计算得到高斯过程如下图。
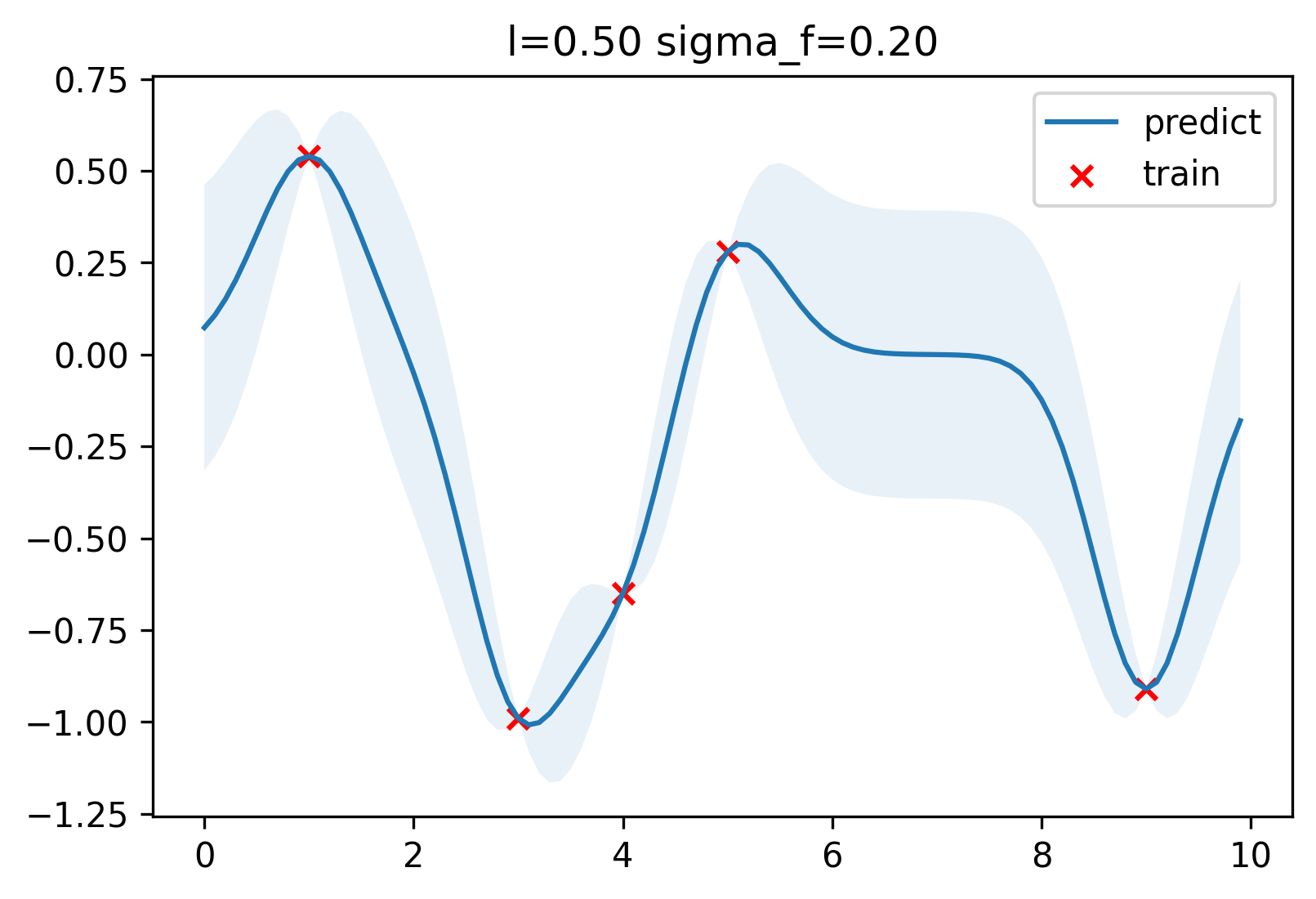
重点:对于每一个新数据点 \(x'\) 都能计算得到该点的函数值的值的分布,而不是单个预测值。含有已知数据(训练集)的地方,variance很低,没有数据的时候,这个spread就比较大。换句话说,越靠近数据集中的点预测的把握就越大。
2.2 核函数
协方差函数又称为核函数,核函数有很多种。通常使用经典的高斯核函数,即: \[ k\left(x, x^{\prime}\right)=\sigma_{f}^{2} \exp \left[\frac{-\left(x-x^{\prime}\right)^{2}}{2 l^{2}}\right] \] 上式中的 \(x,x'\) 为1.2中的时间轴点 \(t,t'\) 。其中 \(\sigma_{f},l\) 为超参数,影响模型的效果,因此使用高斯过程回归需要对这两个参数进行调节(极大似然估计)。
重点:如果两个x比较相似(离得比较近),那么对应的y值的相关性也就较高。换言之,协方差函数是 x的函数(而不是y的函数)。换句话说,协方差函数对应的两个x值的一个相似性度量。
2.3 计算过程
根据上例,对于给定数据集X、Y的情况,计算新的数据点 \(x_{*}=6\) 的预测分布情况。
首先 ,选择合适的u(均值函数)和k(核函数),均值函数一般设为0,核函数一般选择高斯核函数。
其次 ,计算出训练样本( \(K\) )、训练样本与预测样本( \(K*\) )和预测样本( \(K**\) )的核矩阵,如下: \[ K=\begin{bmatrix} 0.040 & 0.000 & 0.010 & 0.000 & 0.000 \\ 0.000 & 0.040 & 0.000 & 0.000 & 0.000 \\ 0.010 & 0.000 & 0.040 & 0.010 & 0.000 \\ 0.000 & 0.000 & 0.010 & 0.040 & 0.000 \\ 0.000 & 0.000 & 0.000 & 0.000 & 0.040 \end{bmatrix} \\ K*=[0.00\quad 0.00\quad 0.00\quad 0.01\quad 0.00],\quad K**=0.04 \] 再次 ,根据公式计算 \(y*\) 的分布。
整个样本的多维高斯分布表达式为(均值函数为0,协方差矩阵为根据核函数计算出的分快矩阵):
\[ \left[\begin{array}{c} \mathbf{y} \\\ y_{*} \end{array}\right] \sim \mathcal{N}\left(\mathbf{0},\left[\begin{array}{cc} K & K_{*}^{\mathrm{T}} \\\ K_{*} & K_{* *} \end{array}\right]\right) \] 根据贝叶斯公式: \[ \begin{align*} p(y^{*} \mid Y) &= \frac{p(Y, y^{*})}{p(Y)}\\\ &= N\left(\mu_{y_{*}}+K_{*} K^{-1}\left(y-\mu_{y}\right), K_{* *}-K_{*} K^{-1} K_{*}^{T}\right)\\\ &= N\left(K_{*} K^{-1}y, K_{* *}-K_{*} K^{-1} K_{*}^{T}\right) \end{align*} \] 其中, \(K,K*,K**\) 根据 \(X\) 计算得出, \(Y\) 为训练集的目标值, \(y*\) 为要计算的 \(x*\) 的目标值分布。
最后 ,根据极大似然估计求解超参数,表达式如下: \[ \begin{align*} \theta&=argmax(\log p(\mathbf{Y} \mid \mathbf{X}, \boldsymbol{\theta})) \\\ &=argmax(-\frac{1}{2} \mathbf{Y}^{\mathrm{T}} K^{-1} \mathbf{Y}-\frac{1}{2} \log |K|-\frac{n}{2} \log 2 \pi) \end{align*} \]
3 总结
(以下内容为个人总结,由于能力有限,如有错误可留言指正)
神经学派中的基于神经网络的深度学习方法通过自身拟合能力通过覆盖密度较大的数据进行训练。在数据足够大的情况下通过对误差的惩罚训练,其本身过拟合问题可以通过一些技术手段(例如正则化、Dropout等)得到较好的解决。因此在数据量较大的情况下神经网络方法能取得较好的效果。
相对于神经网络方法,高斯过程回归更适用于数据量较小的情况。基于高斯核函数的高斯过程回归基于概率统计学,使用小量数据集为参考数据,使用概率的方法通过非线性高斯核函数基于贝叶斯推断在每个数据点进行概率“弥散”,其结果得到平滑的均值曲线与预测点的概率分布,其本身具有非常强的抗过拟合能力。但是由于计算复杂度较高,对于大量数据很难进行计算。对于实时控制领域,计算的时间也很重要,有时计算时间较长而计算结果比较精准的情况未必好于计算时间短而计算结果精准较差的控制效果。
参考资料
[1]快速入门高斯过程回归预测. https://zhuanlan.zhihu.com/p/331591492
[2]浅谈高斯过程回归. https://zhuanlan.zhihu.com/p/76314366
[3]高斯过程和贝叶斯最优化. https://zhuanlan.zhihu.com/p/86386926
[4]参数模型与非参数模型. https://zhuanlan.zhihu.com/p/350307389
[5]高斯过程原理、可视化及代码实现. https://zhuanlan.zhihu.com/p/75589452
[6]An Introduction to Gaussian Process Models. https://arxiv.org/pdf/2102.05497.pdf
[7]高斯过程与高斯过程回归. https://zhuanlan.zhihu.com/p/484128423
附录
附录1:数组转Latex矩阵代码
def array_to_bmatrix(array):
begin = '\\begin{bmatrix} \n'
data = ''
for line in array:
if line.size == 1:
data = data + ' %.2f &'%line
data = data + r' \\'
data = data + '\n'
continue
for idx, element in enumerate(line):
if(idx == len(line)- 1):
data = data + ' %.2f'%element
continue
data = data + ' %.2f &'%element
data = data + r' \\'
data = data + '\n'
end = '\end{bmatrix}'
print(begin + data + end)附录2:简单GPR Python代码
from scipy.optimize import minimize
import numpy as np
class GPR:
def __init__(self, optimize=True):
self.is_fit = False
self.train_X, self.train_y = None, None
self.params = {"l": 0.5, "sigma_f": 0.2}
self.optimize = optimize
def fit(self, X, y):
# store train data
self.train_X = np.asarray(X)
self.train_y = np.asarray(y)
self.is_fit = True
def predict(self, X):
if not self.is_fit:
print("GPR Model not fit yet.")
return
X = np.asarray(X)
Kff = self.kernel(self.train_X, self.train_X) # (N, N)
Kyy = self.kernel(X, X) # (k, k)
Kfy = self.kernel(self.train_X, X) # (N, k)
Kff_inv = np.linalg.inv(Kff + 1e-8 * np.eye(len(self.train_X))) # (N, N)
mu = Kfy.T.dot(Kff_inv).dot(self.train_y)
cov = Kyy - Kfy.T.dot(Kff_inv).dot(Kfy)
return mu, cov
def kernel(self, x1, x2):
dist_matrix = np.sum(x1**2, 1).reshape(-1, 1) + np.sum(x2**2, 1) - 2 * np.dot(x1, x2.T)
return self.params["sigma_f"] ** 2 * np.exp(-0.5 / self.params["l"] ** 2 * dist_matrix)
def y(x, noise_sigma=0.0):
x = np.asarray(x)
y = np.cos(x) + np.random.normal(0, noise_sigma, size=x.shape)
y = np.around(y, 2)
return y.tolist()
import matplotlib.pyplot as plt
train_X = np.array([3, 1, 4, 5, 9]).reshape(-1, 1)
train_y = y(train_X, noise_sigma=1e-4)
test_X = np.arange(0, 10, 0.1).reshape(-1, 1)
gpr = GPR()
gpr.fit(train_X, train_y)
mu, cov = gpr.predict(test_X)
test_y = mu.ravel()
uncertainty = 1.96 * np.sqrt(np.diag(cov))
plt.figure(dpi=300)
plt.title("l=%.2f sigma_f=%.2f" % (gpr.params["l"], gpr.params["sigma_f"]))
plt.fill_between(test_X.ravel(), test_y + uncertainty, test_y - uncertainty, alpha=0.1)
plt.plot(test_X, test_y, label="predict")
plt.scatter(train_X, train_y, label="train", c="red", marker="x")
plt.legend()