1 贝叶斯公式

贝叶斯公式是贝叶斯线性回归的基础，所以我们先来了解下贝叶斯公式： $$ p(\theta \mid X)=\frac{p(X \mid \theta)\times p(\theta)}{p(X)} $$ 在回归问题中$X$表示为数据集$data$，则贝叶斯公式也可表示为： $$ p(\theta \mid data)=\frac{p(data \mid \theta)\times p(\theta)}{p(data)} $$ 其中：

$p(\theta \mid data)$ 为通过样本$data$得到参数$\theta$的概率，即后验概率；

$p(data \mid \theta)$ 为通过参数$\theta$到样本$data$的概率，即似然函数；

$p(\theta)$ 一般根据人的先验知识来得出，即先验概率。

2 参数估计方法¹

2.1 MLE - 最大似然估计

对于样本$X$，我们假设最优的参数$\theta$应当满足：参数$\theta$对应的概率分布中获取到样本$data$的可能性最大，即： $$ \begin{aligned} \hat{\theta}_{\text {MLE }} &=\arg \max P(X \mid \theta) \\ &=\arg \max P\left(x_{1} \mid \theta\right) P\left(x_{2} \mid \theta\right) \cdots P\left(x_{n} \mid \theta\right) \\ &=\arg \max \sum_{i=1}^{n} \log P\left(x_{i} \mid \theta\right) \\ &=\arg \min -\sum_{i=1}^{n} \log P\left(x_{i} \mid \theta\right) \end{aligned} $$

重点：对于参数$\theta$为一个概率分布，因此对于以一个概率分布为条件概率在给定确定值$x$的概率$ P\left(x_{i} \mid \theta\right)$也为一个概率分布。以高斯分布为例，似然分布为多个高斯分布乘积，因此若数据点离散程度越低，多个高斯分布相乘得到的似然高斯分布的方差越小。

2.2 MAP - 最大后验估计

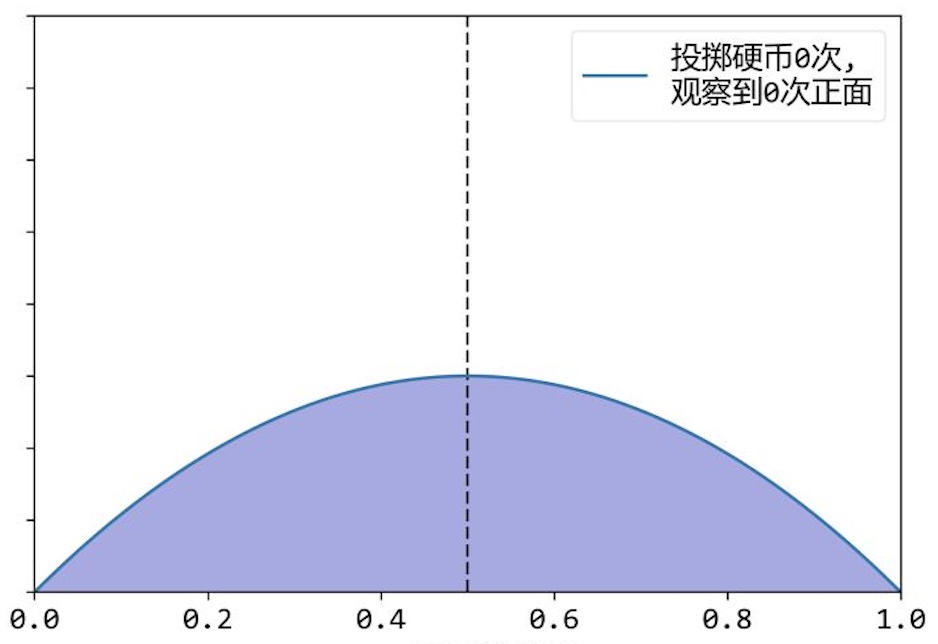
最大后验估计考虑到了先验概率分布，后验概率分布$P(\theta \mid X)$表示为观测到数据集$X$时，参数$\theta$的概率分布，因此可能性最大的参数$\theta$可由如下公式计算： $$ \begin{aligned} \hat{\theta}_{\mathrm{MAP}} &=\arg \max P(\theta \mid X) \\ &=\arg \max( p(X \mid \theta)\times p(\theta)) \\ &=\arg \min -\log P(X \mid \theta)-\log P(\theta)+\log P(X) \\ &=\arg \min -\log P(X \mid \theta)-\log P(\theta) \end{aligned} $$ 以抛硬币为例 ² ，当投抛掷硬币0次时，假设先验概率分布为$p(\theta)=\theta(1-\theta)$，$\theta$为得到正面的概率，即$\theta=0.5$的概率最高，如下图所示。

当投抛掷硬币1次时，得到结果为正面时，根据贝叶斯公式： $$ p(\theta \mid X)=\frac{p(X \mid \theta)\times p(\theta)}{p(X)} $$ 先验概率分布$p(\theta)$与在$\theta$的各个取值下得到正面的概率相乘，得到后验概率的分布大致如下图所示。

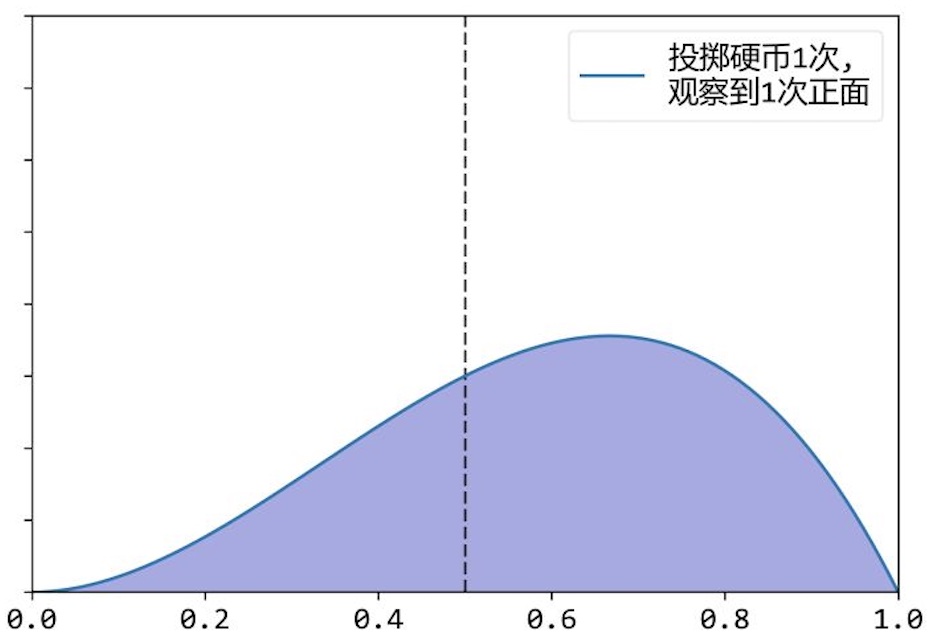
由于$p(X)$的值未知，因此上述图像的高度为估计图像，但是不影响我们求概率最大的参数值。

根据$\hat{\theta}_{\mathrm{MAP}} =\arg \max P(\theta \mid X)=\arg \max( p(X \mid \theta)\times p(\theta))$即可求得概率最高的参数$\theta$。

以此类推，当抛掷硬币10次、100次得到结果为正面时，图像如下图所示。

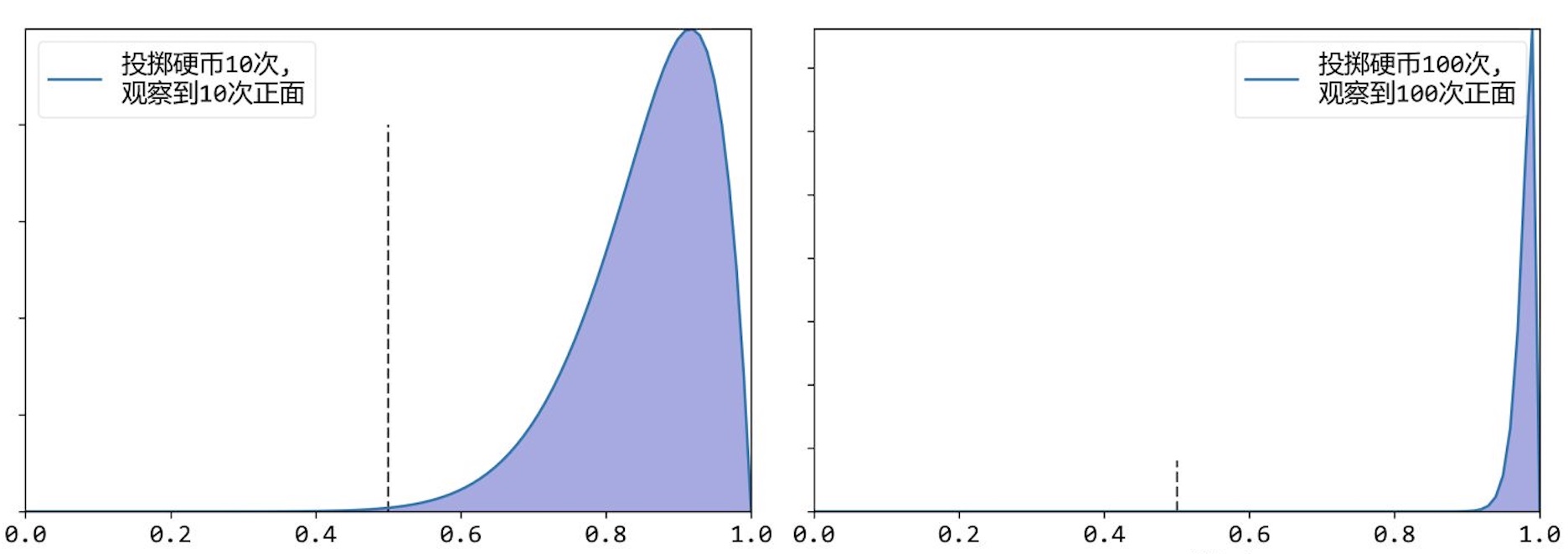
最大后验概率得到的参数$\theta$越来接近1。

3 线性回归问题³

3.1 什么是线性回归问题

故名思意，线性回归是一种线性模型，线性模型形式简单、易于建模。许多功能更为强大的非线性模型可在线性模型的基础上通过引入层级结构或者高维映射而得。

以二维线性回归为例，如下图所示。

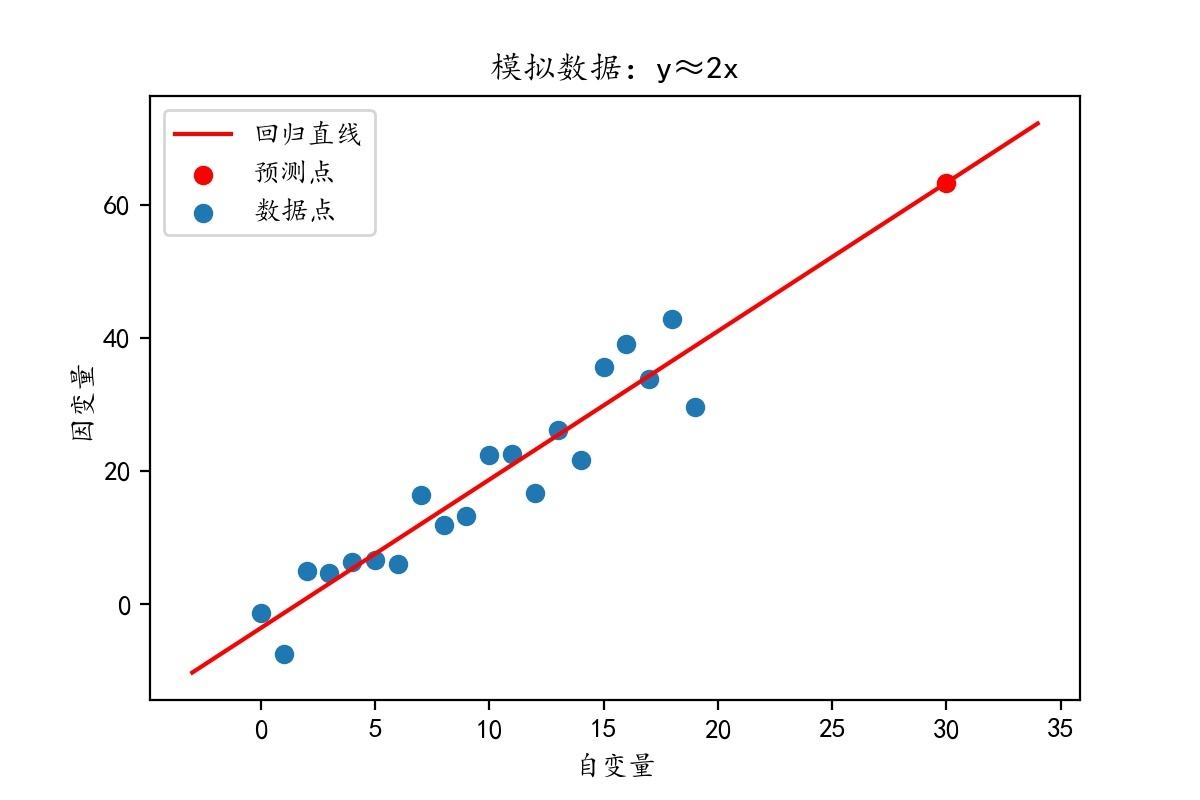
线性回归模型的目的是计算一条直线$y=\theta_1 x+\theta_2$，求解最优参数$\theta_1,\theta_2$使得直线最符合数据的分布趋势，以此来对新的数据点$x_i$进行预测得到$y_i$的值。

通过公式表示为，给定一个训练集（未加转置则为列向量，$x_i为$$d$维列向量，$x_1=1$）： $$ X=\left[\begin{array}{lll} x_{1} & \cdots & x_{n} \end{array}\right]^{T}=\left[\begin{array}{c} x_{1}^{T} \\ \vdots \\ x_{n}^{T} \end{array}\right] \quad x \in \mathbb{R}^{d} $$ 和样本的标签： $$ Y=\left[\begin{array}{lll} y_{1} & \cdots & y_{n} \end{array}\right]^{T} \quad y \in \mathbb{R} $$ 线性回归试图学得一个线性模型： $$ f(x)=w^{T} x, \quad w \in \mathbb{R}^{d} $$ 能够根据给定的$x$以尽可能准确的输出预测值，上面的$w$是模型的参数。

3.2 最小二乘法（最小均方差估计）

最小二乘法求的最优模型参数$w$时，定义一个损失函数： $$ L(w)=\sum_{i=1}^{n}\left(w^{T} x_{i}-y_{i}\right)^{2} $$ 通过最小化损失来得到最优参数。如下图所示，橙色虚线表示为单个样本的损失值。

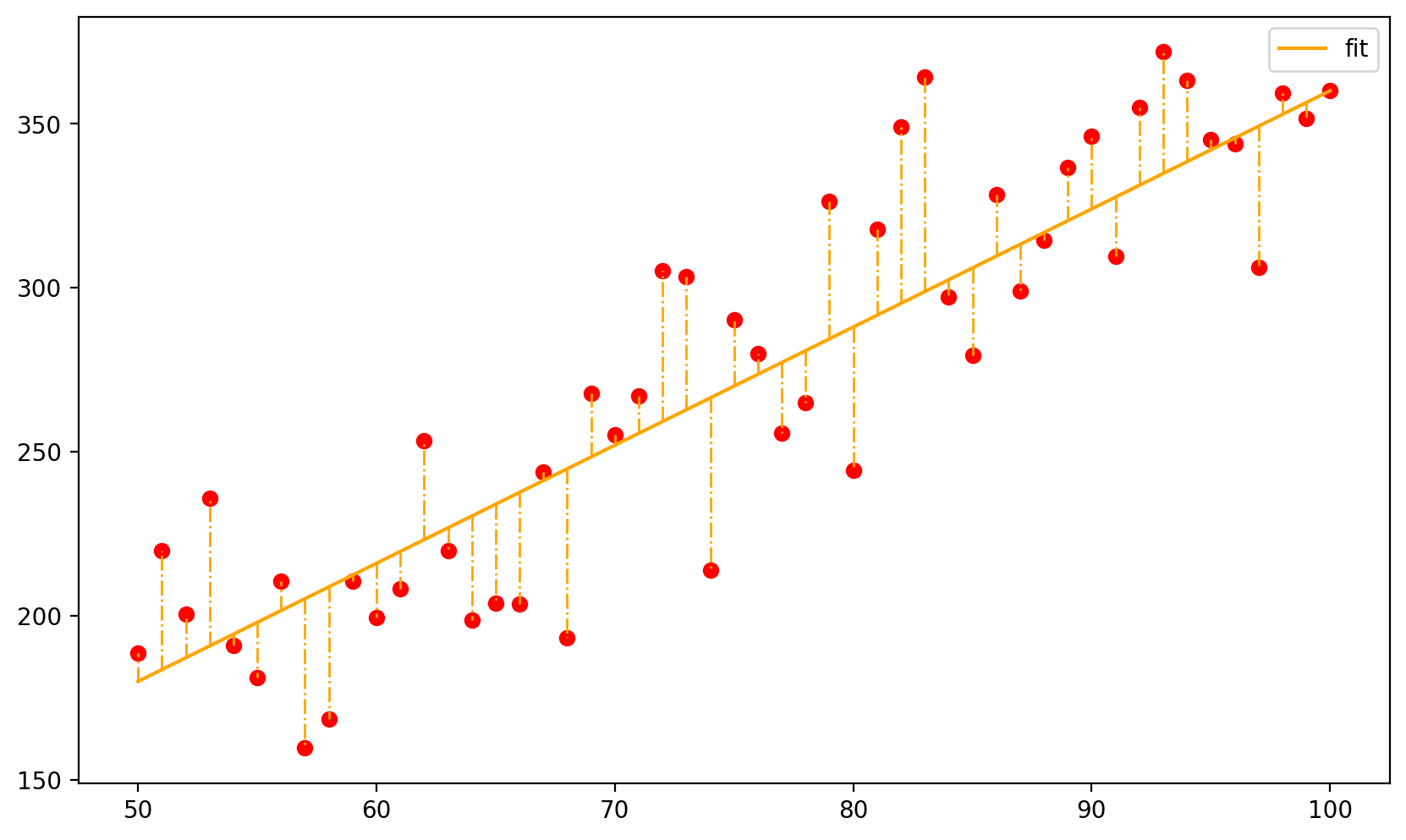
求得满足损失最小时的参数$w$即为所求参数，表示为： $$ w=\arg \min L(w)=\arg \min\sum_{i=1}^{n}\left(w^{T} x_{i}-y_{i}\right)^{2} $$ 求解上式只需代入数值对$w$求导数并令导数为0即可，最小二乘法不是本文重点具体计算过程不在赘述。

3.3 极大似然估计求解线性回归

对于样本拟合直线之间的误差也可用一个高斯噪声表示，即$\epsilon \sim \mathcal{N}\left(0, \sigma^{2}\right)$，公式表示为： $$ y=w^{T} x+\epsilon $$ $y$的均值$\mathbb{E}[y]=w^{T} x$，方差$\operatorname{Var}[y]=\sigma^{2}$，即：$y \sim \mathcal{N}\left(w^{T} x, \sigma^{2}\right)$。

此时的未知参数包括：参数$w$和误差的方差$\sigma^{2}$，定义对数似然函数： $$ \begin{aligned} \ell(w) &=\log P(Y \mid X, w) \\ &=\log \prod_{i=1}^{n} P\left(y_{i} \mid x_{i}, w\right) \\ &=\log \prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{1}{2 \sigma}\left(y_{i}-w^{T} x\right)^{2}\right) \\ &=\log \frac{1}{(2 \pi)^{\frac{n}{2}} \sigma^{n}}+\sum_{i}^{n}\left(-\frac{1}{2 \sigma}\left(y_{i}-w^{T} x\right)^{2}\right) \end{aligned} $$ 可以看到，参数$\sigma$在常数项中，不影响我们求得最优解，因此： $$ \begin{aligned} \hat{w} &=\arg \max \ell(w) \\ &=\arg \max \log \frac{1}{(2 \pi)^{\frac{n}{2}} \sigma^{n}}+\sum_{i}^{n}\left(-\frac{1}{2 \sigma}\left(y_{i}-w^{T} x_{i}\right)^{2}\right) \\ &=\arg \max -\frac{1}{2 \sigma} \sum_{i}^{n}\left(y_{i}-w^{T} x_{i}\right)^{2} \\ &=\arg \min \sum_{i}^{n}\left(y_{i}-w^{T} x_{i}\right)^{2} \\ &=\arg \min L(w) \end{aligned} $$ 结果与最小二乘法一致。

重点：极大似然求解最优值表示为存在一个参数$w$，在给定$w,X$的情况下得到$Y$的概率最大。

3.4 贝叶斯线性回归

贝叶斯线性回归与前面相同，即： $$ y=w^{T} x+\epsilon $$ $y$的均值$\mathbb{E}[y]=w^{T} x$，方差$\operatorname{Var}[y]=\sigma^{2}$，即：$y \sim \mathcal{N}\left(w^{T} x, \sigma^{2}\right)$。

重点：使用贝叶斯线性回归采用最大后验估计，因此要假设一个先验分布。因此，$w$并非一个固定值，而是一个分布，我们假设$w$的先验分布为高斯分布，即$w \sim \mathcal{N}(0, \Sigma)$。

首先，通过贝叶斯公式： $$ \begin{aligned} P(w \mid Y, X) &=\frac{P(Y, X, w)}{P(Y, X)} \\ &=\frac{P(Y \mid X, w) P(X \mid w) P(w)}{P(Y, X)} \\ & \propto P(Y \mid X, w) P(w) \end{aligned} $$ 其中，$P(Y \mid X, w)$为在3.3的极大似然估计，其分布为正态分布。

$P(w)$为预先假设的高斯分布，即$w \sim \mathcal{N}(0, \Sigma)$。

根据高斯分布的共轭性，其后验分布$P(w \mid Y, X)$也为高斯分布，其表达式为： $$ \begin{aligned} P(Y \mid X, w) P(w) &=C \exp \left(-\frac{1}{2 \sigma^{2}}(Y-X w)^{T}(Y-X w)\right) \exp \left(-\frac{1}{2} w^{T} \Sigma^{-1} w\right) \\ &=C \exp \left(-\frac{1}{2 \sigma^{2}}(Y-X w)^{T}(Y-X w)-\frac{1}{2} w^{T} \Sigma^{-1} w\right) \end{aligned} $$

重点：对于后验概率分布的表达式中忽略了其中的常数项，那怎么求的后验分布的具体值呢？根据后验概率分布为高斯分布这一信息，我们假设后验分布服从$(w \mid Y, X) \sim \mathcal{N}\left(\mu_{w}, \Sigma_{w}\right)$。而对于高斯分布，只需要知道其均值和方差即可确定其分布，而均值和方差根据指数部分即可确定，而指数部分已知。

通过化简配方，求的后验分布的参数值： $$ \begin{aligned} \Sigma_{w}^{-1}&=\sigma^{-2} X^{T} X+\Sigma^{-1} \\ \mu_{w}&=\sigma^{-2} \Sigma_{w} X^{T} Y \end{aligned} $$ 对一个新的样本$x$的$y$值进行预测： $$ y=x^{T} w+\epsilon $$ 因为$\epsilon \sim \mathcal{N}\left(0, \sigma^{2}\right)$, 所以 $ y \sim \mathcal{N}\left(x^{T} \mu_{w}, x^{T} \Sigma_{w} x+\sigma^{2}\right)$。

重点：对于贝叶斯线性回归，我们并未对参数$w$进行估计，而是使用$w$其本身的概率分布用来计算预测值，因此在不同概率下$w$的值不同，预测得到的$y$值也不同，因此预测得到的并非一个点，而是一个分布。

4 总结

（个人能力有限，学习结论可能存在若干错误，若发现错误可联系我修正）

在频率学派看来，存在一个参数$w$使得曲线对样本的拟合程度最优，即仅考虑最优解；

在贝叶斯学派看来，参数$w$的概率本身也服从一定分布，即后验概率分布，对于最大后验估计为取概率最大的$w$作为估计。重点是：由于先验分布的存在，概率最大的参数$w$未必是拟合程度最优的参数$w$，或者说永远也达不到最优的参数$w$，而是随着数据量大增加无限逼近（参考2.2投掷硬币例子）。

因此，贝叶斯估计的优点是在数据量较小时可以充分利用先验知识定义的先验分布，以至于不会出现重大错误结果；缺点是由于先验分布与真实分布的误差，后验分布逼近最优解但是无法真正到达最优解。

对于贝叶斯线性回归，在回归过程中并未对参数$w$进行估计，而是将$w$视为一个概率分布，因此得到的预测值也是一个概率分布。

附录

附录1：matplotlib绘图

# 产生数据
def generate():
    x = np.linspace(50, 100, 51)
    w = 3.6
    y = w * x + np.random.normal(0, 30, size=x.size)
    X = x.reshape(-1,1)
    Y = y.reshape(-1,1)
    return X, Y

X, Y = generate()

plt.figure(dpi = 500, figsize = (10,6)) # 设置图片DPI与大小
plt.scatter(X, Y, c='r') # 绘制数据散点图
line, = plt.plot(X, 3.6*X, color='orange') # 绘制回归直线

# 绘制直线与散点连线
for i in range(0, len(Y)):
    plt.plot([X[i], X[i]], [3.6*X[i], Y[i]], linewidth=1, color='orange',ls='-.')

# 绘制legend
plt.legend(handles=[line], labels=['fit'], loc='best')
plt.show()

$$ \downarrow $$

附录2：贝叶斯线代回归Python代码实现³

import numpy as np
import matplotlib.pyplot as plt

def generate():
    x = np.linspace(50, 150)
    w = 3.6
    y = w * x + np.random.normal(0, 30, size=x.size)
    X = x.reshape(-1,1)
    Y = y.reshape(-1,1)
    return X, Y

class LinearRegression(object):
    def __init__(self, w=None):
        self.w = w

    def least_square(self, X, Y):
        '''
        最小二乘法，通过给定样本学习参数
        X: 样本矩阵，一行一样本
        Y: 样本标签，Nx1矩阵
        '''
        inv = np.linalg.inv(np.dot(X.T, X))
        self.w = inv.dot(np.dot(X.T, Y))
        
    def ridge(self, X, Y, lam=3e-2):
        # 岭回归
        inv = np.linalg.inv(np.dot(X.T, X) + np.diag([lam]*X.shape[-1]))
        self.w = inv.dot(np.dot(X.T, Y))

    def predict(self, x):
        '''
        通过给定数据进行预测
        '''
        return np.dot(x, self.w)


class BayesRegression(object):
    def __init__(self, sigma, mu=None, cov=None):
        self.sigma = sigma  # 噪声方差
        self.mu = mu        # 后验分布的均值
        self.cov = cov      # 后验分布的协方差矩阵

    def fit(self, X, Y):
        '''
        拟合后验参数
        '''
        prior = np.eye(X.shape[-1])     # 先验协方差
        A = np.dot(X.T, X) / self.sigma
        self.cov = np.linalg.inv(A)
        self.mu = self.cov.dot(np.dot(X.T, Y)) / self.sigma

    def generate(self, x):
        '''
        根据给定数据，生成预测值
        '''
        mean = np.dot(x, self.mu).sum()
        std = np.sqrt(np.dot(x, self.cov).dot(x)).sum()
        return np.random.normal(mean, std, 1)

    def generate_random(self, x):
        '''
        根据给定数据，生成带噪声的预测值
        '''
        mean = np.dot(x, self.mu).sum()
        std = np.sqrt(np.dot(x, self.cov).dot(x) + self.sigma).sum()
        return np.random.normal(mean, std, 1)
        

def main():
    X, Y = generate()
    lr = LinearRegression()
    lr.ridge(X, Y)
    x = np.array([50, 150]).reshape(-1,1)
    y = lr.predict(x)

    plt.figure()
    plt.scatter(X, Y)
    plt.plot(x, y, c='r')
    for i, j in zip(X, Y):
        plt.plot([i,i], [j, lr.predict(i)], c='b', linestyle='dotted')
    plt.show()


if __name__ == "__main__":
    # main()
    X, Y = generate()
    lr = LinearRegression()
    lr.least_square(X, Y)
    sigma = np.square(Y - np.dot(X, lr.w)).mean()
    '''
    关于贝叶斯线性回归需要将噪声的方差传给模型，但是计算方差又需要具体的w值
    所以没办法只能通过判别模型的线性回归拟合w，然后再计算噪声的方差
    '''
    br = BayesRegression(sigma)
    br.fit(X, Y)
    
    xx = []
    yy = []
    count = 30
    for x in np.linspace(50, 150):
        xx += [x] * count
        yy += [br.generate_random(x) for _ in range(count)]
    
    plt.figure(figsize=(21,9))
    plt.scatter(xx, yy, c='r')
    plt.show()